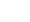Simplify Cube Root of 5312

Here we will show you step-by-step how to simplify the cube root of 5312. Before we continue, note that the cube root of 5312 can be written as follows:

∛5312

The ∛ symbol is called the radical sign. To simplify the cube root of 5312 means to get the simplest radical form of ∛5312.

Step 1: List Factors
We start by listing the factors of 5312 like so:

1, 2, 4, 8, 16, 32, 64, 83, 166, 332, 664, 1328, 2656, and 5312

Step 2: Find Perfect Cubes
Next, we identify the perfect cubes* from the list of factors above:

1, 8, and 64

Step 3: Find the number to go inside the radical
From the list of perfect cubes, you see that 64 is the largest perfect cube. Now, divide 5312 by the largest perfect cube to find the number that will go inside the radical.

5312 / 64 = 83

Step 4: Find the number to go outside the radical
To find the number that will go outside the radical, we simply calculate the cube root of the largest perfect cube:

∛64 = 4

Step 5: Get the answer
Put Steps 3 and 4 together to get the cube root of 5312 in its simplest radical form. You put the result from Step 3 inside the radical and the result from Step 4 outside the radical:

4∛83

There you have it folks! Now you know how to simplify the cube root of 5312. The answer to the cube root of 5312 in its simplest radical form is displayed below:

∛5312 = 4∛83

Simplify Cube Root Calculator
Please enter another cube root for us to simplify:

Decimal Form
When we entered the cube root of 5312 into our calculator, we got the answer to the cube root of 5312 in decimal form:

∛5312 ≈ 17.4483

Exponent Form
Here is how to write the cube root of 5312 written with an exponent instead of a radical:

5312^⅓ = 4 × 83^⅓

Simplify Cube Root of 5313
The answer to "simplify cube root of 5312" is not the only problem we have solved. Go here for the next problem on our list.

* List of Perfect Cubes