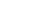Simplify Cube Root of 108

Here we will show you step-by-step how to simplify the cube root of 108. Before we continue, note that the cube root of 108 can be written as follows:

∛108

The ∛ symbol is called the radical sign. To simplify the cube root of 108 means to get the simplest radical form of ∛108.

Step 1: List Factors
We start by listing the factors of 108 like so:

1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108

Step 2: Find Perfect Cubes
Next, we identify the perfect cubes* from the list of factors above:

1 and 27

Step 3: Find the number to go inside the radical
From the list of perfect cubes, you see that 27 is the largest perfect cube. Now, divide 108 by the largest perfect cube to find the number that will go inside the radical.

108 / 27 = 4

Step 4: Find the number to go outside the radical
To find the number that will go outside the radical, we simply calculate the cube root of the largest perfect cube:

∛27 = 3

Step 5: Get the answer
Put Steps 3 and 4 together to get the cube root of 108 in its simplest radical form. You put the result from Step 3 inside the radical and the result from Step 4 outside the radical:

3∛4

There you have it folks! Now you know how to simplify the cube root of 108. The answer to the cube root of 108 in its simplest radical form is displayed below:

∛108 = 3∛4

Simplify Cube Root Calculator
Please enter another cube root for us to simplify:

Decimal Form
When we entered the cube root of 108 into our calculator, we got the answer to the cube root of 108 in decimal form:

∛108 ≈ 4.7622

Exponent Form
Here is how to write the cube root of 108 written with an exponent instead of a radical:

108^⅓ = 3 × 4^⅓

Simplify Cube Root of 109
The answer to "simplify cube root of 108" is not the only problem we have solved. Go here for the next problem on our list.

* List of Perfect Cubes