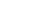Simplify Square Root of 68

Here we will show you step-by-step how to simplify the square root of 68. The square root of 68 can be written as follows:


	√	68

The √ symbol is called the radical sign. To simplify the square root of 68 means to get the simplest radical form of √68.

Step 1: List Factors
List the factors of 68 like so:

1, 2, 4, 17, 34, 68

Step 2: Find Perfect Squares
Identify the perfect squares* from the list of factors above:

1, 4

Step 3: Divide
Divide 68 by the largest perfect square you found in the previous step:

68 / 4 = 17

Step 4: Calculate
Calculate the square root of the largest perfect square:

√4 = 2

Step 5: Get Answer
Put Steps 3 and 4 together to get the square root of 68 in its simplest form:


2	√	17

Simplify Square Root Calculator
Please enter another Square Root for us to simplify:

Decimal Form
Square Root of 68 in Decimal form rounded to nearest 5 decimals:

8.24621

Exponent Form
Square Root of 68 written with Exponent instead of Radical:

68^½ = 2 x 17^½

Simplify Square Root of 69
The answer to Simplify Square Root of 68 is not the only problem we solved. Go here for the next problem on our list.

* List of Perfect Squares