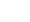Simplify Square Root of 1025

Here we will show you step-by-step how to simplify the square root of 1025. The square root of 1025 can be written as follows:


	√	1025

The √ symbol is called the radical sign. To simplify the square root of 1025 means to get the simplest radical form of √1025.

Step 1: List Factors
List the factors of 1025 like so:

1, 5, 25, 41, 205, 1025

Step 2: Find Perfect Squares
Identify the perfect squares* from the list of factors above:

1, 25

Step 3: Divide
Divide 1025 by the largest perfect square you found in the previous step:

1025 / 25 = 41

Step 4: Calculate
Calculate the square root of the largest perfect square:

√25 = 5

Step 5: Get Answer
Put Steps 3 and 4 together to get the square root of 1025 in its simplest form:


5	√	41

Simplify Square Root Calculator
Please enter another Square Root for us to simplify:

Decimal Form
Square Root of 1025 in Decimal form rounded to nearest 5 decimals:

32.01562

Exponent Form
Square Root of 1025 written with Exponent instead of Radical:

1025^½ = 5 x 41^½

Simplify Square Root of 1026
The answer to Simplify Square Root of 1025 is not the only problem we solved. Go here for the next problem on our list.

* List of Perfect Squares