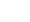4x + 2y = 12

Here we will show you how to calculate and provide solutions to math problems related to 4x + 2y = 12.

We will start by calculating and showing you the solution for the x-intercept and y-intercept of 4x + 2y = 12.

Then, we will show you how to get the graph plot coordinates for 4x + 2y = 12 so we can illustrate it on a graph.

Finally, we will solve 4x + 2y = 12 for x and also for y, then calculate and show you the solution for the slope of 4x + 2y = 12.

Find x-intercept
The x-intercept is where the graph crosses the x-axis. To find the x-intercept, we set y₁=0 and then solve for x.

4x + 2y = 12
4x + 2(0) = 12
x₁ = 3 y₁ = 0

Find y-intercept
The y-intercept is where the graph crosses the y-axis. To find the y-intercept, we set x₂=0 and then solve for y.

4x + 2y = 12
4(0) + 2y = 12
y₂ = 6 x₂ = 0

Get Graph Plot Coordinates
Getting two graph points will allow you to make a straight line on a graph. The plot coordinate format is (x₁,y₁) and (x₂,y₂).

Thus, we use the x-intercept and y-intercept results above to get the graph plots for 4x + 2y = 12 as follows:

(x₁,y₁) and (x₂,y₂)
(3,0) and (0,6)

Solve for x
To solve for x, we solve the equation so the variable x is by itself on the left side:

4x + 2y = 12
x = 3 - 0.5y

Solve for y
To solve for y, we solve the equation so the variable y is by itself on the left side:

4x + 2y = 12
y = 6 - 2x

Find slope
The slope of the line (m) is the steepness of the line. It is the change in the y coordinate divided by the corresponding change in the x coordinate. Simply plug in the coordinates from above and solve for m to get the slope for 4x + 2y = 12

m = (y₂ - y₁)/(x₂ - x₁)
m = (6 - 0)/(0 - 3)
m = -2

Ax + By = C Calculator
Now you know how to solve 4x + 2y = 12. Enter another math problem here: